Проекции графики: различия между версиями

Материал из Posmotrelisu
Перейти к навигации Перейти к поиску
 
(Новая страница: «thumb|right|250px '''Проекция графики''' — способ отобразить трёхмерный игровой мир на плоском экране. Проекции бывают: * Параллельные — проецирующие прямые параллельны: ** Ортогональные — проецирующие прямые перпендикулярны экрану; ** К...»)
Строка 1: Строка 1:
[[Файл:Типы проекций.png|thumb|right|250px]]
[[Файл:Типы проекций.png|thumb|right|250px]]
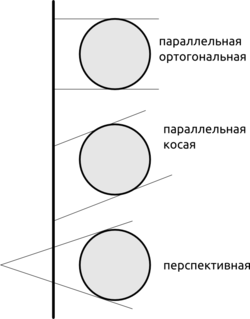
'''Проекция графики''' — способ отобразить трёхмерный игровой мир на плоском экране.
'''Проекция графики''' — способ отобразить трёхмерный игровой мир на плоском экране.


Проекции бывают:
Проекции бывают:
* Параллельные — проецирующие прямые параллельны:
* Параллельные — проецирующие прямые параллельны:
** Ортогональные — проецирующие прямые перпендикулярны экрану;
** Ортогональные — проецирующие прямые перпендикулярны экрану;
** Косые — соответственно, не перпендикулярны;
** Косые — соответственно, не перпендикулярны;
* Перспективные — проецирующие прямые сходятся в одной точке:
* Перспективные — проецирующие прямые сходятся в одной точке:
** Одноточечная — картинная плоскость параллельна одной из граней;
** Одноточечная — картинная плоскость параллельна одной из граней;
** Двухточечная — картинная плоскость всегда вертикальна;
** Двухточечная — картинная плоскость всегда вертикальна;
** Трёхточечная — картинная плоскость произвольная;
** Трёхточечная — картинная плоскость произвольная;
* Ломаная перспектива — отсутствие единой проекции как художественный приём.
* Ломаная перспектива — отсутствие единой проекции как художественный приём.


Необоснованный разнобой проекций — известная ошибка игровых художников. В одной из мобильных игр автор этих строк (работавший утилитчиком и консультантом по движку) насчитал четыре разных проекции: плоскую, «три четверти» снизу, «три четверти» сверху и диметрическую.
Необоснованный разнобой проекций — известная ошибка игровых художников. В одной из мобильных игр автор этих строк (работавший утилитчиком и консультантом по движку) насчитал четыре разных проекции: плоскую, «три четверти» снизу, «три четверти» сверху и диметрическую.


== Параллельные проекции (2D) ==
== Параллельные проекции (2D) ==


Параллельные проекции называются «2D» потому, что проекция предмета не зависит от его координат. Поэтому изображения можно подготовить заранее, в виде двухмерных спрайтов. Но в этом же и засада — нужны дополнительные визуальные подсказки, где по оси Z объект (это замечательно обыграно в ''[[Fez]]''). Из собственного опыта: в 2006-м разработали для мобильников (на Java ME) несложную 3D-головоломку — шарик прыгает по конструкции из кубиков, висящей в космосе. Но только для тех, которые поддерживают 3D (их немного, наобум некоторые Nokia и Sony Ericsson). Решили сделать такое же для 2D-мобильников — в аксонометрии. Написали прототип и бросили — неиграбельно, не поймёшь, как стоят эти кубики.
Параллельные проекции называются «2D» потому, что проекция предмета не зависит от его координат. Поэтому изображения можно подготовить заранее, в виде двухмерных спрайтов. Но в этом же и засада — нужны дополнительные визуальные подсказки, где по оси Z объект (это замечательно обыграно в ''[[Fez]]''). Из собственного опыта: в 2006-м разработали для мобильников (на Java ME) несложную 3D-головоломку — шарик прыгает по конструкции из кубиков, висящей в космосе. Но только для тех, которые поддерживают 3D (их немного, наобум некоторые Nokia и Sony Ericsson). Решили сделать такое же для 2D-мобильников — в аксонометрии. Написали прототип и бросили — неиграбельно, не поймёшь, как стоят эти кубики.
** Ну играли же люди как-то в Qbert-а...
** Ну играли же люди как-то в Qbert-а...


Строка 25: Строка 25:
==== Плоская ====
==== Плоская ====


[[Файл:SuperMarioBros.png|frame|right|Большинство двухмерных игр используют именно плоскую проекцию. На скриншоте — [[Super Mario Bros.]]]]
[[Файл:SuperMarioBros.png|frame|right|Большинство двухмерных игр используют именно плоскую проекцию. На скриншоте — [[Super Mario Bros.]]]]
Самая тупая из проекций — уровень выглядит как на [[Справочник Автора/Механика|чертеже]] в разрезе. Но заодно и самая «экономная» и потому применяется там, где надо блеснуть разнообразием ландшафтов или сложным геймплеем, а графические красоты приберечь.
Самая тупая из проекций — уровень выглядит как на [[Справочник Автора/Механика|чертеже]] в разрезе. Но заодно и самая «экономная» и потому применяется там, где надо блеснуть разнообразием ландшафтов или сложным геймплеем, а графические красоты приберечь.
<br clear="all" />
<br clear="all" />


==== «Три четверти» ====
==== «Три четверти» ====


[[Файл:Три четверти кубик.png|thumb|right|400px|Проекция «три четверти». Слева — косой вариант, справа — прямой. Различия, как видно, невелики. Для тех, кто в танке: косоту смотрят не по кубику, а по линиям, проецирующим его на экран.]]
[[Файл:Три четверти кубик.png|thumb|right|400px|Проекция «три четверти». Слева — косой вариант, справа — прямой. Различия, как видно, невелики. Для тех, кто в танке: косоту смотрят не по кубику, а по линиям, проецирующим его на экран.]]
Другими словами — «в фас и немного сверху».
Другими словами — «в фас и немного сверху».


Трудно сказать, чем считать проекцию «три четверти» — косой или ортогональной. Ортогональная проекция отличается от косой сжатым масштабом по оси Y. Но всё-таки разница между тем и другим невелика<ref>Если быть точным, cos α, который даже для 30° будет 0,86. Малая грань уже 0,5 — а большая всё ещё 0,86!</ref> — так что пускай будет «условно прямая».
Трудно сказать, чем считать проекцию «три четверти» — косой или ортогональной. Ортогональная проекция отличается от косой сжатым масштабом по оси Y. Но всё-таки разница между тем и другим невелика<ref>Если быть точным, cos α, который даже для 30° будет 0,86. Малая грань уже 0,5 — а большая всё ещё 0,86!</ref> — так что пускай будет «условно прямая».


Проекцией «три четверти» известен, например, ''[[WarCraft/Warcraft II|WarCraft II]]''. Была очень популярна в ранних jRPG эпохи NES и SNES, например, ''[[Final Fantasy]]'' c I по VI; сейчас её использует инструментарий для создания jRPG серии [[RPG Maker]], продолжающий те традиции.
Проекцией «три четверти» известен, например, ''[[WarCraft/Warcraft II|WarCraft II]]''. Была очень популярна в ранних jRPG эпохи NES и SNES, например, ''[[Final Fantasy]]'' c I по VI; сейчас её использует инструментарий для создания jRPG серии [[RPG Maker]], продолжающий те традиции.
Строка 43: Строка 43:
[[Файл:Изометрия кубик.png|thumb|left|120px|Изометрическая проекция]]
[[Файл:Изометрия кубик.png|thumb|left|120px|Изометрическая проекция]]
[[Файл:UFO изометрия.png|frame|right|''[[X-COM: UFO Defense]]''; изометрическая проекция с ромбическими плитками. В оригинале использовался режим 320×200 с неквадратным пикселем, и картинка не была так безжалостно сплющена по вертикали.]]
[[Файл:UFO изометрия.png|frame|right|''[[X-COM: UFO Defense]]''; изометрическая проекция с ромбическими плитками. В оригинале использовался режим 320×200 с неквадратным пикселем, и картинка не была так безжалостно сплющена по вертикали.]]
'''Аксонометрической''' называется параллельная проекция, у которой все три оси переходят в разные прямые. '''Изометрическая''' проекция — аксонометрическая с одинаковым масштабом по всем осям. Из всех аксонометрических проекций особенно важна — и в черчении, и в играх — '''прямоугольная изометрическая''' (зачастую просто «изометрическая»): проектирующие прямые параллельны вектору (1, 1, 1).
'''Аксонометрической''' называется параллельная проекция, у которой все три оси переходят в разные прямые. '''Изометрическая''' проекция — аксонометрическая с одинаковым масштабом по всем осям. Из всех аксонометрических проекций особенно важна — и в черчении, и в играх — '''прямоугольная изометрическая''' (зачастую просто «изометрическая»): проектирующие прямые параллельны вектору (1, 1, 1).


Ось Z в изометрии смотрит на 12 часов (вертикально вверх), остальные две — на 4 и 8 часов (на 30° от горизонтали). Впрочем, часто используют «почти изометрию» со ступенчатыми линиями 2:1 — это даёт угол arctg 0,5 ≈ 26,57°.
Ось Z в изометрии смотрит на 12 часов (вертикально вверх), остальные две — на 4 и 8 часов (на 30° от горизонтали). Впрочем, часто используют «почти изометрию» со ступенчатыми линиями 2:1 — это даёт угол arctg 0,5 ≈ 26,57°.


'''Интересно''': в режимах 320<span style="margin-left:0.1em; margin-right:0.1em">×</span>200 пиксель вытянут по вертикали. Это идеальное соотношение для изометрии: и числа круглые, и соотношение 2:1 даёт угол 30,96°<ref>= arctg[ 0,5·320·3 / (200·4) ]. Коэффициенты 3 и 4 — из соотношения сторон экрана 4:3.</ref>. Скорее всего, так вышло ненамеренно, в попытках сесть на два стула — и пристойный текст, и выход на NTSC (да, CGA имел выход на NTSC).
'''Интересно''': в режимах 320<span style="margin-left:0.1em; margin-right:0.1em">×</span>200 пиксель вытянут по вертикали. Это идеальное соотношение для изометрии: и числа круглые, и соотношение 2:1 даёт угол 30,96°<ref>= arctg[ 0,5·320·3 / (200·4) ]. Коэффициенты 3 и 4 — из соотношения сторон экрана 4:3.</ref>. Скорее всего, так вышло ненамеренно, в попытках сесть на два стула — и пристойный текст, и выход на NTSC (да, CGA имел выход на NTSC).


Изометрические игры, в свою очередь, делятся на игры с ромбическими [[тайлсет|плитками]] (''[[X-COM: UFO Defense]]'') и на игры с квадратными плитками (''[[StarCraft]]''). В целом считается, что ромбические плитки хороши для автоматической генерации уровня (''[[X-COM: UFO Defense]]'', ''[[Diablo]]'') и для явно изометрической механики (''[[X-COM: UFO Defense]]'', ''[[Knight Lore]]'', ''[[Spindizzy]]''), квадратные — для реалистичного вида при редактировании вручную. Плюс расходуют меньше памяти.
Изометрические игры, в свою очередь, делятся на игры с ромбическими [[тайлсет|плитками]] (''[[X-COM: UFO Defense]]'') и на игры с квадратными плитками (''[[StarCraft]]''). В целом считается, что ромбические плитки хороши для автоматической генерации уровня (''[[X-COM: UFO Defense]]'', ''[[Diablo]]'') и для явно изометрической механики (''[[X-COM: UFO Defense]]'', ''[[Knight Lore]]'', ''[[Spindizzy]]''), квадратные — для реалистичного вида при редактировании вручную. Плюс расходуют меньше памяти.
<br clear="all" />
<br clear="all" />


Строка 55: Строка 55:


[[Файл:Nether Earth.gif|frame|right|[[Nether Earth]]. Если быть буквоедом, это косая проекция, но «косота» мало заметна.]]
[[Файл:Nether Earth.gif|frame|right|[[Nether Earth]]. Если быть буквоедом, это косая проекция, но «косота» мало заметна.]]
Прочие ортогональные аксонометрические проекции встречаются крайне редко — обычно в головоломках и стратегиях.
Прочие ортогональные аксонометрические проекции встречаются крайне редко — обычно в головоломках и стратегиях.
<br clear="all" />
<br clear="all" />


=== Косые ===
=== Косые ===


В косых проекциях направление проецирования — под углом к экрану.
В косых проекциях направление проецирования — под углом к экрану.


==== Диметрическая ====
==== Диметрическая ====


[[Файл:Prince of Persia.gif|frame|right|[[Prince of Persia]] — игра в диметрической проекции. Снова-таки, не обращайте внимание на сжатую картинку: использовался всё тот же режим 320×200 с неквадратным пикселем. И обратите внимание на Принца в плоской проекции.]]
[[Файл:Prince of Persia.gif|frame|right|[[Prince of Persia]] — игра в диметрической проекции. Снова-таки, не обращайте внимание на сжатую картинку: использовался всё тот же режим 320×200 с неквадратным пикселем. И обратите внимание на Принца в плоской проекции.]]
Если '''изо'''метрическая подразумевает одинаковые масштабы по всем осям, в '''ди'''метрической два масштаба — один по двум осям, и другой по третьей. Диметрическая проекция бывает фронтальной и ортогональной. Если ортогональная используется крайне редко, то '''фронтальная диметрическая''' (более простая, но косая<ref>Кто чертил: ось X, которая во фронтальной проекции горизонтальная, в ортогональной наклонена на 7°.</ref>) широко применяется в двухмерных играх, как в горизонтальном разрезе, так и в вертикальном, давая суррогат трёхмерности. Масштаб по третьей оси — 50 %.
Если '''изо'''метрическая подразумевает одинаковые масштабы по всем осям, в '''ди'''метрической два масштаба — один по двум осям, и другой по третьей. Диметрическая проекция бывает фронтальной и ортогональной. Если ортогональная используется крайне редко, то '''фронтальная диметрическая''' (более простая, но косая<ref>Кто чертил: ось X, которая во фронтальной проекции горизонтальная, в ортогональной наклонена на 7°.</ref>) широко применяется в двухмерных играх, как в горизонтальном разрезе, так и в вертикальном, давая суррогат трёхмерности. Масштаб по третьей оси — 50 %.


Персонажей, бегающих по уровню, обычно в диметрию не переводят, а рисуют в традиционной плоской проекции (или в «три четверти»).
Персонажей, бегающих по уровню, обычно в диметрию не переводят, а рисуют в традиционной плоской проекции (или в «три четверти»).
Строка 73: Строка 73:


[[Файл:Планиметрия кубик.png|thumb|120px|Планиметрическая проекция]]
[[Файл:Планиметрия кубик.png|thumb|120px|Планиметрическая проекция]]
Та же диметрическая, но повёрнутая на 135°. Ею пользуются очень немногие игры, в основном jRPG и стратегии. На приставках с «лежачим» пикселем проекция становится ближе к ортогональной, на компьютерах со «стоячим»<ref>Конечно, имеются в виду приставки и компьютеры тех времён (начало 90-х). 640×480 VGA, 800×600 SVGA и всё, что появилось позднее — это белые и пушистые квадратные пиксели.</ref> — наоборот, портится. В связи с особенностями нашего зрения масштаб по оси Z может быть как классические 50 %, так и поменьше.
Та же диметрическая, но повёрнутая на 135°. Ею пользуются очень немногие игры, в основном jRPG и стратегии. На приставках с «лежачим» пикселем проекция становится ближе к ортогональной, на компьютерах со «стоячим»<ref>Конечно, имеются в виду приставки и компьютеры тех времён (начало 90-х). 640×480 VGA, 800×600 SVGA и всё, что появилось позднее — это белые и пушистые квадратные пиксели.</ref> — наоборот, портится. В связи с особенностями нашего зрения масштаб по оси Z может быть как классические 50 %, так и поменьше.
<br clear="all" />
<br clear="all" />


Строка 80: Строка 80:
В перспективных проекциях, как уже говорилось, проецирующие прямые пересекаются в «объективе» виртуальной камеры.
В перспективных проекциях, как уже говорилось, проецирующие прямые пересекаются в «объективе» виртуальной камеры.


Поскольку экран ограничен, у перспективной проекции есть два важных параметра — фокусное расстояние (в «условных миллиметрах») и угол зрения (от 0 до 180°). Они взаимосвязаны: между углом зрения φ и фокусным расстоянием ''d'' соотношение
Поскольку экран ограничен, у перспективной проекции есть два важных параметра — фокусное расстояние (в «условных миллиметрах») и угол зрения (от 0 до 180°). Они взаимосвязаны: между углом зрения φ и фокусным расстоянием ''d'' соотношение


: ''d'' = ½ ''w'' ctg (φ/2),
: ''d'' = ½ ''w'' ctg (φ/2),


где ''w'' — ширина стандартного фотоматериала (36 мм). На старых трубчатых мониторах угол зрения ставят 90° или чуть меньше, современные (2014) 16:10 могут отобразить без дискомфорта до 120°.
где ''w'' — ширина стандартного фотоматериала (36 мм). На старых трубчатых мониторах угол зрения ставят 90° или чуть меньше, современные (2014) 16:10 могут отобразить без дискомфорта до 120°.
* Большой угол зрения (= малое фокусное расстояние): вид с малого расстояния, преувеличенная перспектива, сильные искажения по краям, мелкий масштаб
* Большой угол зрения (= малое фокусное расстояние): вид с малого расстояния, преувеличенная перспектива, сильные искажения по краям, мелкий масштаб
* Малый угол зрения (= большое фокусное расстояние): вид издали с большим увеличением, сжатая перспектива, незаметные искажения картинки, крупный масштаб
* Малый угол зрения (= большое фокусное расстояние): вид издали с большим увеличением, сжатая перспектива, незаметные искажения картинки, крупный масштаб
Строка 93: Строка 93:
[[Файл:Трёхточечная проекция.png|thumb|left|240px|Почему трёхточечная]]
[[Файл:Трёхточечная проекция.png|thumb|left|240px|Почему трёхточечная]]
[[Файл:Дюрер лютня.jpg|thumb|right|240px|Альбрехт Дюрер. «Построение перспективы лютни». Самое настоящее low-tech 3D.]]
[[Файл:Дюрер лютня.jpg|thumb|right|240px|Альбрехт Дюрер. «Построение перспективы лютни». Самое настоящее low-tech 3D.]]
Собственно, настоящая «трёхмерная» проекция называется '''трёхточечной''', с лёгкой руки художников, которые где-то за рамкой картины выбирают три точки схода и делают, чтобы продолжения линий пересекались в этих трёх точках. Разумеется, компьютер никаких точек схода не расставляет — они получаются автоматически, если честно прокрутить 3D-расчёты.
Собственно, настоящая «трёхмерная» проекция называется '''трёхточечной''', с лёгкой руки художников, которые где-то за рамкой картины выбирают три точки схода и делают, чтобы продолжения линий пересекались в этих трёх точках. Разумеется, компьютер никаких точек схода не расставляет — они получаются автоматически, если честно прокрутить 3D-расчёты.


3D использовалось в серии Final Fantasy эпохи PSX (VII—IX) для трехмерных моделей героев, монстров и NPC, а также фонов в боевых сценах; для всего остального использовались нарисованные в той же проекции статичные 2D-задники. Начиная с десятки, серия стала полностью трёхмерной и лишилась прибитой гвоздями камеры.
3D использовалось в серии Final Fantasy эпохи PSX (VII—IX) для трехмерных моделей героев, монстров и NPC, а также фонов в боевых сценах; для всего остального использовались нарисованные в той же проекции статичные 2D-задники. Начиная с десятки, серия стала полностью трёхмерной и лишилась прибитой гвоздями камеры.
Строка 105: Строка 105:
Если картинная плоскость вертикальна, любая вертикальная прямая останется вертикальной (остаются только две точки схода). Опыт художников показывает, что наш мозг успешно корректирует вертикальную перспективу, и здания и интерьеры, показанные в статике в трёхточечной проекции, смотрятся плохо. Поэтому на картинах делают только две точки схода, а вертикальные линии оставляют вертикальными. Фотографы, снимающие здания, корректируют перспективу фотошопом или шифт-объективом.
Если картинная плоскость вертикальна, любая вертикальная прямая останется вертикальной (остаются только две точки схода). Опыт художников показывает, что наш мозг успешно корректирует вертикальную перспективу, и здания и интерьеры, показанные в статике в трёхточечной проекции, смотрятся плохо. Поэтому на картинах делают только две точки схода, а вертикальные линии оставляют вертикальными. Фотографы, снимающие здания, корректируют перспективу фотошопом или шифт-объективом.


А чем она интересна для нас, геймеров? А тем, что в годы с 1992 по 1996 она процветала в 3D-играх. [[Wolfenstein 3D]], [[Doom]], [[Duke Nukem 3D]] и многие другие трёхмерные игры того времени использовали двухточечную проекцию и рисовали стены по столбцам, а полы — по строкам.
А чем она интересна для нас, геймеров? А тем, что в годы с 1992 по 1996 она процветала в 3D-играх. [[Wolfenstein 3D]], [[Doom]], [[Duke Nukem 3D]] и многие другие трёхмерные игры того времени использовали двухточечную проекцию и рисовали стены по столбцам, а полы — по строкам.
{{main|Псевдотрёхмерность}}
{{main|Псевдотрёхмерность}}
<br clear="all" />
<br clear="all" />
Строка 111: Строка 111:
=== Одноточечная ===
=== Одноточечная ===


[[Файл:AticAtac.png|frame|''[[Atic Atac]]'' — здание в одноточечной проекции (для экономии памяти изрядно «поломанной»), а персонажи внезапно с видом сбоку.]]
[[Файл:AticAtac.png|frame|''[[Atic Atac]]'' — здание в одноточечной проекции (для экономии памяти изрядно «поломанной»), а персонажи внезапно с видом сбоку.]]
Последняя разновидность перспективной проекции — когда картинной плоскости параллельны аж два ребра (то есть, одна грань). Раз две точки схода удалены в бесконечность, остаётся только одна — в направлении взгляда (обычно, но не обязательно, в центре картины).
Последняя разновидность перспективной проекции — когда картинной плоскости параллельны аж два ребра (то есть, одна грань). Раз две точки схода удалены в бесконечность, остаётся только одна — в направлении взгляда (обычно, но не обязательно, в центре картины).


В 2D-играх одноточечной перспективой делают только внутренности зданий. Персонажей и объекты обычно рисуют в проекции «три четверти» или боковой — даже если взгляд сверху вниз. Естественно, перспектива пригодна в основном для поэкранного фона; чтобы на прокручивающемся фоне артефакты не были заметны, художнику нужно хорошее чувство перспективы.
В 2D-играх одноточечной перспективой делают только внутренности зданий. Персонажей и объекты обычно рисуют в проекции «три четверти» или боковой — даже если взгляд сверху вниз. Естественно, перспектива пригодна в основном для поэкранного фона; чтобы на прокручивающемся фоне артефакты не были заметны, художнику нужно хорошее чувство перспективы.


Современные [[ремейк]]и классических игр (''[[Prince of Persia]] Classic'', ''[[Duck Tales]] Remastered'') переводят в 3D с одноточечной проекцией.
Современные [[ремейк]]и классических игр (''[[Prince of Persia]] Classic'', ''[[Duck Tales]] Remastered'') переводят в 3D с одноточечной проекцией.


Ещё примеры.
Ещё примеры.
* ''[[Prince of Persia]] 2: The Shadow and the Flame'' выполнена в традиционной диметрии с плоскими спрайтами, но одна из [[Видеовставка|сцен на движке]] — {{spoiler|«Avenge us! Avenge us!»}} — в одноточечной перспективе.
* ''[[Prince of Persia]] 2: The Shadow and the Flame'' выполнена в традиционной диметрии с плоскими спрайтами, но одна из [[Видеовставка|сцен на движке]] — {{spoiler|«Avenge us! Avenge us!»}} — в одноточечной перспективе.
* ''[[Another World]]'' в отдельных экранах использует одноточечную перспективу.
* ''[[Another World]]'' в отдельных экранах использует одноточечную перспективу.
* Существуют и псевдотрёхмерные игры с одноточечной проекцией, наиболее известные из них ''[[Grand Theft Auto]]'' 1 и 2.
* Существуют и псевдотрёхмерные игры с одноточечной проекцией, наиболее известные из них ''[[Grand Theft Auto]]'' 1 и 2.
Строка 137: Строка 137:


== Ломаная перспектива ==
== Ломаная перспектива ==
[[Файл:SuperContraЛоманая.jpg|thumb|right|240px|Ломаная проекция в ''[[Contra|Super Contra]]''. Стены — попытались сделать какую-то перспективу, края платформ — «три четверти», узор на платформе — диметрия.]]
[[Файл:SuperContraЛоманая.jpg|thumb|right|240px|Ломаная проекция в ''[[Contra|Super Contra]]''. Стены — попытались сделать какую-то перспективу, края платформ — «три четверти», узор на платформе — диметрия.]]
В ломаной проекции вообще нет проецирующих прямых: одни объекты проецируются так, другие этак. Это неплохо разнообразит 2D-игру, однако требует от художника опыта: нужно чувствовать перспективу и понимать габариты экрана, знать, что игрок увидит часто, что — редко, а что — вообще не увидит.
В ломаной проекции вообще нет проецирующих прямых: одни объекты проецируются так, другие этак. Это неплохо разнообразит 2D-игру, однако требует от художника опыта: нужно чувствовать перспективу и понимать габариты экрана, знать, что игрок увидит часто, что — редко, а что — вообще не увидит.


Причин «поломать» проекцию много.
Причин «поломать» проекцию много.
* Художественные причины:
* Художественные причины:
** Чтобы сгладить искажения проекции. Шар в любой косой проекции будет эллипсом — так, понятное дело, нельзя, мячик должен быть круглым. ''Atic Atac'' (см. выше) явно «снят широкоугольным объективом», и по краям «кадра» искажения будут слишком велики. Потому картины переданы в другой проекции.
** Чтобы сгладить искажения проекции. Шар в любой косой проекции будет эллипсом — так, понятное дело, нельзя, мячик должен быть круглым. ''Atic Atac'' (см. выше) явно «снят широкоугольным объективом», и по краям «кадра» искажения будут слишком велики. Потому картины переданы в другой проекции.
** Чтобы передать смену проекции при прокрутке уровня.
** Чтобы передать смену проекции при прокрутке уровня.
** Для небольших предметов, которые невозможно нарисовать в такой проекции. Правда, если у машины широкая палитра, можно попробовать передать проекцию удачным тонированием.
** Для небольших предметов, которые невозможно нарисовать в такой проекции. Правда, если у машины широкая палитра, можно попробовать передать проекцию удачным тонированием.
** И просто «желание левой задней пятки художника» aka «художественная выразительность».
** И просто «желание левой задней пятки художника» aka «художественная выразительность».
* Технические причины:
* Технические причины:
** Экономия памяти или работы художника (например, в плоской или 3/4 правый поворот — [[двурукий спрайт|зеркальное отражение]] левого, а в диметрии — нет).
** Экономия памяти или работы художника (например, в плоской или 3/4 правый поворот — [[двурукий спрайт|зеркальное отражение]] левого, а в диметрии — нет).
** Совместимость с различными компьютерными технологиями: [[тайлсет|плиточный фон]], [[картонная анимация|«картонная» анимация]]<ref>Анимация, когда персонаж состоит из плоских сочленённых деталей, как картонная кукла. Детали могут быть нежёсткими и деформироваться (как в портретах [[Dust: An Elysian Tail]]).</ref>…
** Совместимость с различными компьютерными технологиями: [[тайлсет|плиточный фон]], [[картонная анимация|«картонная» анимация]]<ref>Анимация, когда персонаж состоит из плоских сочленённых деталей, как картонная кукла. Детали могут быть нежёсткими и деформироваться (как в портретах [[Dust: An Elysian Tail]]).</ref>…


[[w:Перспектива#Обратная линейная перспектива|Обратная перспектива]], распространённая в средневековой иллюстрации и иконописи, тоже ломаная. Изредка её используют и в играх — для построек намного больших, чем экран. В жизни подобие обратной перспективы встречается, если какой-нибудь объект находится в сантиметрах от носа — между глаз.
[[w:Перспектива#Обратная линейная перспектива|Обратная перспектива]], распространённая в средневековой иллюстрации и иконописи, тоже ломаная. Изредка её используют и в играх — для построек намного больших, чем экран. В жизни подобие обратной перспективы встречается, если какой-нибудь объект находится в сантиметрах от носа — между глаз.
<br clear="all" />
<br clear="all" />


== Параллаксная (многослойная) прокрутка ==
== Параллаксная (многослойная) прокрутка ==
{{youtube|uWhJOIFKtm8|Кто не играл в «[[Aladdin|Аладдин]]а» на «сеге»? Обратите внимание на барханы и облака на заднем плане — это один слой, но с фирменной «полосатой» прокруткой}}
{{youtube|uWhJOIFKtm8|Кто не играл в «[[Aladdin|Аладдин]]а» на «сеге»? Обратите внимание на барханы и облака на заднем плане — это один слой, но с фирменной «полосатой» прокруткой}}
[[w:Параллакс|Параллакс]] — это видимое смещение объектов друг относительно друга, когда смещается зритель. Самый впечатляющий параллакс будет, если посмотреть из окна автобуса или поезда. Следующий наш метод моделирует это явление.
[[w:Параллакс|Параллакс]] — это видимое смещение объектов друг относительно друга, когда смещается зритель. Самый впечатляющий параллакс будет, если посмотреть из окна автобуса или поезда. Следующий наш метод моделирует это явление.


Устроена параллаксная прокрутка несложно, этот метод освоили ещё мультипликаторы. Берём несколько слоёв (все, кроме нижнего — с прозрачными «дырками») и перемещаем их с разной скоростью, получается неплохая иллюзия перспективы. Сами же слои редко делают перспективными — обычно в какой-нибудь из параллельных проекций.
Устроена параллаксная прокрутка несложно, этот метод освоили ещё мультипликаторы. Берём несколько слоёв (все, кроме нижнего — с прозрачными «дырками») и перемещаем их с разной скоростью, получается неплохая иллюзия перспективы. Сами же слои редко делают перспективными — обычно в какой-нибудь из параллельных проекций.


Super Nintendo (он же SNES) позволял до четырёх слоёв, Sega Megadrive (она же Sega Genesis) — всего два, но могла независимо прокручивать полосы фона<ref>По поводу того, чем приставки отличаются от ПК: [http://prog21.dadgum.com/181.html статья], [http://mercury13-kiev.livejournal.com/40783.html перевод]</ref>. На ПК многослойная прокрутка возможна, начиная с 386-х машин<ref>Скроллинг был и на «двойках» (''[[Golden Axe]]''), но делался он хитрым перепрограммированием VGA по рецептам небезызвестного [[w:Абраш, Майкл|Майкла Абраша]] и не позволял «дыр». Другими словами, однослойный. А на полную перерисовку экрана 286-м не хватало пропускной способности шины.</ref>. Из JavaME-телефонов (во времена их максимального распространения, середина 2000-х) многослойную прокрутку поддерживали только самые шустрые<ref>То же самое: [[w:Кольцевой буфер|особым образом забуферизировав фон]], можно наладить очень быструю прокрутку, даже на Samsung C100 дававшую ≈8 fps — но без дыр.</ref>.
Super Nintendo (он же SNES) позволял до четырёх слоёв, Sega Megadrive (она же Sega Genesis) — всего два, но могла независимо прокручивать полосы фона<ref>По поводу того, чем приставки отличаются от ПК: [http://prog21.dadgum.com/181.html статья], [http://mercury13-kiev.livejournal.com/40783.html перевод]</ref>. На ПК многослойная прокрутка возможна, начиная с 386-х машин<ref>Скроллинг был и на «двойках» (''[[Golden Axe]]''), но делался он хитрым перепрограммированием VGA по рецептам небезызвестного [[w:Абраш, Майкл|Майкла Абраша]] и не позволял «дыр». Другими словами, однослойный. А на полную перерисовку экрана 286-м не хватало пропускной способности шины.</ref>. Из JavaME-телефонов (во времена их максимального распространения, середина 2000-х) многослойную прокрутку поддерживали только самые шустрые<ref>То же самое: [[w:Кольцевой буфер|особым образом забуферизировав фон]], можно наладить очень быструю прокрутку, даже на Samsung C100 дававшую ≈8 fps — но без дыр.</ref>.


В [[квест (жанр)|квестах]] фирмы Daedalic Entertainment (''[[The Whispered World]]'', ''[[Deponia]]'') таких слоёв может быть более десятка. Правда, это уже 2000-е годы…
В [[квест (жанр)|квестах]] фирмы Daedalic Entertainment (''[[The Whispered World]]'', ''[[Deponia]]'') таких слоёв может быть более десятка. Правда, это уже 2000-е годы…


В 3D параллакс получается автоматически. Однако, чтобы не рисовать много далёких объектов, используют так называемый [[w:скайбокс|скайбокс]] — большой задник, малоподвижный по сравнению со всеми остальными игровыми объектами. Старые FPS наподобие ''[[Doom]]'' заливали экран особой текстурой, когда движок попадал на «небесные» стены. В современных играх скайбокс — очень отдалённый, но существующий в геометрии уровней задник.
В 3D параллакс получается автоматически. Однако, чтобы не рисовать много далёких объектов, используют так называемый [[w:скайбокс|скайбокс]] — большой задник, малоподвижный по сравнению со всеми остальными игровыми объектами. Старые FPS наподобие ''[[Doom]]'' заливали экран особой текстурой, когда движок попадал на «небесные» стены. В современных играх скайбокс — очень отдалённый, но существующий в геометрии уровней задник.
<br clear="all" />
<br clear="all" />


Строка 173: Строка 173:
* Имитация плохой оптики (множество оптических приборов ''[[Myst]]'', шлем Большого Папочки в ''[[BioShock]]'').
* Имитация плохой оптики (множество оптических приборов ''[[Myst]]'', шлем Большого Папочки в ''[[BioShock]]'').


С развитием шейдеров стали делать локальные искажения, связанные с преломлением в воде или перегретом воздухе — но это уже не проекция.
С развитием шейдеров стали делать локальные искажения, связанные с преломлением в воде или перегретом воздухе — но это уже не проекция.


== Трактат о неквадратном пикселе ==
== Трактат о неквадратном пикселе ==
Строка 179: Строка 179:
Выше много раз говорилось: пиксель неквадратный, должно быть вытянуто (или, наоборот, приплюснуто) по вертикали. А почему оно так? Вкратце: ориентация на телевизор и ориентация на текст.
Выше много раз говорилось: пиксель неквадратный, должно быть вытянуто (или, наоборот, приплюснуто) по вертикали. А почему оно так? Вкратце: ориентация на телевизор и ориентация на текст.


Давайте посмотрим несколько распространённых на то время машин (пропорция =1 — квадратный пиксель, &gt;1 — стоячий пиксель, &lt;1 — лежачий).<ref>Методика подсчёта: 0,75·ширина/высота. Для всех японских NTSC-приставок берётся высота 240 (приставкам нужно изображение без рамки, а полный NTSC-растр составляет 483 строки). Об Apple см. в тексте.</ref>
Давайте посмотрим несколько распространённых на то время машин (пропорция =1 — квадратный пиксель, &gt;1 — стоячий пиксель, &lt;1 — лежачий).<ref>Методика подсчёта: 0,75·ширина/высота. Для всех японских NTSC-приставок берётся высота 240 (приставкам нужно изображение без рамки, а полный NTSC-растр составляет 483 строки). Об Apple см. в тексте.</ref>


{| class="wikitable"
{| class="wikitable"
Строка 214: Строка 214:
|}
|}


В PAL- и SÉCAM-машинах около 256 строк, в NTSC- — начиная с 200: одна строка пикселей — это две строки телевизионной развёртки. Горизонтальное же разрешение — столько, сколько вытягивает техника, обычно поменьше, потому и лежачий пиксель. Sega с квадратным пикселем выглядит «монстром» на фоне других машин. К тому же у телевизора развёртка чересстрочная и пиксельное тонирование будет адски полыхать — поэтому в полное телевизионное разрешение вышли уже тогда, когда truecolor-режимы сделали эти «изыски» ненужными (PlayStation, 1995).
В PAL- и SÉCAM-машинах около 256 строк, в NTSC- — начиная с 200: одна строка пикселей — это две строки телевизионной развёртки. Горизонтальное же разрешение — столько, сколько вытягивает техника, обычно поменьше, потому и лежачий пиксель. Sega с квадратным пикселем выглядит «монстром» на фоне других машин. К тому же у телевизора развёртка чересстрочная и пиксельное тонирование будет адски полыхать — поэтому в полное телевизионное разрешение вышли уже тогда, когда truecolor-режимы сделали эти «изыски» ненужными (PlayStation, 1995).


Компьютерам приходится работать с текстом, поэтому горизонтальное разрешение важнее вертикального — а значит, стоячий пиксель. Правда, мониторы могут свободно перестраивать развёртку и потому не привязаны к 200 (или 256) строкам. В крупных шрифтах (например, в шрифтах для текстовых режимов в 8px шириной) вертикальные штрихи делали двухпиксельными.
Компьютерам приходится работать с текстом, поэтому горизонтальное разрешение важнее вертикального — а значит, стоячий пиксель. Правда, мониторы могут свободно перестраивать развёртку и потому не привязаны к 200 (или 256) строкам. В крупных шрифтах (например, в шрифтах для текстовых режимов в 8px шириной) вертикальные штрихи делали двухпиксельными.


А что же Macintosh, явно выбивающийся из нашей таблицы? Кинескоп у него обычный, 4:3. Но он намеренно не использовал полную площадь трубки, чтобы пиксель был в точности квадратный, а плотность была 72 пикселя на дюйм — для удобства настольного издательства. Впоследствии привязка к 72 ppi<ref>''Pixels per inch'', пикселей на дюйм.</ref> сильно ударила по Apple (в Windows, например, принято 96 ppi, но не столь жёстко<ref>Хотя программирование под большие PPI — такой ещё ад, не зря в Windows 7 придумали виртуализацию PPI (программа должна сказать: «Я поддерживаю высокую плотность пикселей», иначе Windows её отрендерит на стандартной и растянет). Но хотя бы разработчики крупного ПО этот ад знают и проходят.</ref>) — но это уже середина 1990-х.<ref>[http://www.artlebedev.ru/kovodstvo/sections/70/ Ководство, § 70. Разрешение экранов. И немного о происхождении 72 точек на дюйм.]</ref>.
А что же Macintosh, явно выбивающийся из нашей таблицы? Кинескоп у него обычный, 4:3. Но он намеренно не использовал полную площадь трубки, чтобы пиксель был в точности квадратный, а плотность была 72 пикселя на дюйм — для удобства настольного издательства. Впоследствии привязка к 72 ppi<ref>''Pixels per inch'', пикселей на дюйм.</ref> сильно ударила по Apple (в Windows, например, принято 96 ppi, но не столь жёстко<ref>Хотя программирование под большие PPI — такой ещё ад, не зря в Windows 7 придумали виртуализацию PPI (программа должна сказать: «Я поддерживаю высокую плотность пикселей», иначе Windows её отрендерит на стандартной и растянет). Но хотя бы разработчики крупного ПО этот ад знают и проходят.</ref>) — но это уже середина 1990-х.<ref>[http://www.artlebedev.ru/kovodstvo/sections/70/ Ководство, § 70. Разрешение экранов. И немного о происхождении 72 точек на дюйм.]</ref>.


''Техническое отступление.'' Развёртка — это процесс управления электронным лучом приёмной телевизионной трубки ([[w:Кинескоп|кинескопа]]). Луч строка за строкой проходит по всему экрану, строя изображение. Развёртка бывает построчной, или прогрессивной (каждый кадр развёртываются все строки одна за другой), и [[w:Чересстрочная развёртка|чересстрочной]] (первый полукадр развёртываются строки 1, 3, 5, 7 и т. д., второй полукадр — 2, 4, 6, 8…).
''Техническое отступление.'' Развёртка — это процесс управления электронным лучом приёмной телевизионной трубки ([[w:Кинескоп|кинескопа]]). Луч строка за строкой проходит по всему экрану, строя изображение. Развёртка бывает построчной, или прогрессивной (каждый кадр развёртываются все строки одна за другой), и [[w:Чересстрочная развёртка|чересстрочной]] (первый полукадр развёртываются строки 1, 3, 5, 7 и т. д., второй полукадр — 2, 4, 6, 8…).


== Примечания ==
== Примечания ==

Версия 18:27, 26 марта 2022

Типы проекций.png

Проекция графики — способ отобразить трёхмерный игровой мир на плоском экране.

Проекции бывают:

  • Параллельные — проецирующие прямые параллельны:
    • Ортогональные — проецирующие прямые перпендикулярны экрану;
    • Косые — соответственно, не перпендикулярны;
  • Перспективные — проецирующие прямые сходятся в одной точке:
    • Одноточечная — картинная плоскость параллельна одной из граней;
    • Двухточечная — картинная плоскость всегда вертикальна;
    • Трёхточечная — картинная плоскость произвольная;
  • Ломаная перспектива — отсутствие единой проекции как художественный приём.

Необоснованный разнобой проекций — известная ошибка игровых художников. В одной из мобильных игр автор этих строк (работавший утилитчиком и консультантом по движку) насчитал четыре разных проекции: плоскую, «три четверти» снизу, «три четверти» сверху и диметрическую.

Параллельные проекции (2D)

Параллельные проекции называются «2D» потому, что проекция предмета не зависит от его координат. Поэтому изображения можно подготовить заранее, в виде двухмерных спрайтов. Но в этом же и засада — нужны дополнительные визуальные подсказки, где по оси Z объект (это замечательно обыграно в Fez). Из собственного опыта: в 2006-м разработали для мобильников (на Java ME) несложную 3D-головоломку — шарик прыгает по конструкции из кубиков, висящей в космосе. Но только для тех, которые поддерживают 3D (их немного, наобум некоторые Nokia и Sony Ericsson). Решили сделать такое же для 2D-мобильников — в аксонометрии. Написали прототип и бросили — неиграбельно, не поймёшь, как стоят эти кубики.

    • Ну играли же люди как-то в Qbert-а...

Ортогональные

В ортогональных (или прямоугольных) проекциях направление проецирования перпендикулярно экрану.

Плоская

Большинство двухмерных игр используют именно плоскую проекцию. На скриншоте — Super Mario Bros.

Самая тупая из проекций — уровень выглядит как на чертеже в разрезе. Но заодно и самая «экономная» и потому применяется там, где надо блеснуть разнообразием ландшафтов или сложным геймплеем, а графические красоты приберечь.

«Три четверти»

Проекция «три четверти». Слева — косой вариант, справа — прямой. Различия, как видно, невелики. Для тех, кто в танке: косоту смотрят не по кубику, а по линиям, проецирующим его на экран.

Другими словами — «в фас и немного сверху».

Трудно сказать, чем считать проекцию «три четверти» — косой или ортогональной. Ортогональная проекция отличается от косой сжатым масштабом по оси Y. Но всё-таки разница между тем и другим невелика[1] — так что пускай будет «условно прямая».

Проекцией «три четверти» известен, например, WarCraft II. Была очень популярна в ранних jRPG эпохи NES и SNES, например, Final Fantasy c I по VI; сейчас её использует инструментарий для создания jRPG серии RPG Maker, продолжающий те традиции.

Изометрическая

Изометрическая проекция
X-COM: UFO Defense; изометрическая проекция с ромбическими плитками. В оригинале использовался режим 320×200 с неквадратным пикселем, и картинка не была так безжалостно сплющена по вертикали.

Аксонометрической называется параллельная проекция, у которой все три оси переходят в разные прямые. Изометрическая проекция — аксонометрическая с одинаковым масштабом по всем осям. Из всех аксонометрических проекций особенно важна — и в черчении, и в играх — прямоугольная изометрическая (зачастую просто «изометрическая»): проектирующие прямые параллельны вектору (1, 1, 1).

Ось Z в изометрии смотрит на 12 часов (вертикально вверх), остальные две — на 4 и 8 часов (на 30° от горизонтали). Впрочем, часто используют «почти изометрию» со ступенчатыми линиями 2:1 — это даёт угол arctg 0,5 ≈ 26,57°.

Интересно: в режимах 320×200 пиксель вытянут по вертикали. Это идеальное соотношение для изометрии: и числа круглые, и соотношение 2:1 даёт угол 30,96°[2]. Скорее всего, так вышло ненамеренно, в попытках сесть на два стула — и пристойный текст, и выход на NTSC (да, CGA имел выход на NTSC).

Изометрические игры, в свою очередь, делятся на игры с ромбическими плитками (X-COM: UFO Defense) и на игры с квадратными плитками (StarCraft). В целом считается, что ромбические плитки хороши для автоматической генерации уровня (X-COM: UFO Defense, Diablo) и для явно изометрической механики (X-COM: UFO Defense, Knight Lore, Spindizzy), квадратные — для реалистичного вида при редактировании вручную. Плюс расходуют меньше памяти.

Прочие аксонометрические

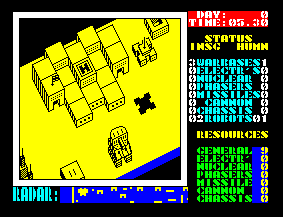
Nether Earth. Если быть буквоедом, это косая проекция, но «косота» мало заметна.

Прочие ортогональные аксонометрические проекции встречаются крайне редко — обычно в головоломках и стратегиях.

Косые

В косых проекциях направление проецирования — под углом к экрану.

Диметрическая

Prince of Persia — игра в диметрической проекции. Снова-таки, не обращайте внимание на сжатую картинку: использовался всё тот же режим 320×200 с неквадратным пикселем. И обратите внимание на Принца в плоской проекции.

Если изометрическая подразумевает одинаковые масштабы по всем осям, в диметрической два масштаба — один по двум осям, и другой по третьей. Диметрическая проекция бывает фронтальной и ортогональной. Если ортогональная используется крайне редко, то фронтальная диметрическая (более простая, но косая[3]) широко применяется в двухмерных играх, как в горизонтальном разрезе, так и в вертикальном, давая суррогат трёхмерности. Масштаб по третьей оси — 50 %.

Персонажей, бегающих по уровню, обычно в диметрию не переводят, а рисуют в традиционной плоской проекции (или в «три четверти»).

Планиметрическая

Планиметрическая проекция

Та же диметрическая, но повёрнутая на 135°. Ею пользуются очень немногие игры, в основном jRPG и стратегии. На приставках с «лежачим» пикселем проекция становится ближе к ортогональной, на компьютерах со «стоячим»[4] — наоборот, портится. В связи с особенностями нашего зрения масштаб по оси Z может быть как классические 50 %, так и поменьше.

Перспективные

В перспективных проекциях, как уже говорилось, проецирующие прямые пересекаются в «объективе» виртуальной камеры.

Поскольку экран ограничен, у перспективной проекции есть два важных параметра — фокусное расстояние (в «условных миллиметрах») и угол зрения (от 0 до 180°). Они взаимосвязаны: между углом зрения φ и фокусным расстоянием d соотношение

d = ½ w ctg (φ/2),

где w — ширина стандартного фотоматериала (36 мм). На старых трубчатых мониторах угол зрения ставят 90° или чуть меньше, современные (2014) 16:10 могут отобразить без дискомфорта до 120°.

  • Большой угол зрения (= малое фокусное расстояние): вид с малого расстояния, преувеличенная перспектива, сильные искажения по краям, мелкий масштаб
  • Малый угол зрения (= большое фокусное расстояние): вид издали с большим увеличением, сжатая перспектива, незаметные искажения картинки, крупный масштаб

И к программированию видео на движке применяются те же правила, что и к обычной фото- и видеосъёмке: так, говорящую голову «снимают» фокусным расстоянием от 70 до 140 мм.

Трёхточечная (3D)

Почему трёхточечная
Альбрехт Дюрер. «Построение перспективы лютни». Самое настоящее low-tech 3D.

Собственно, настоящая «трёхмерная» проекция называется трёхточечной, с лёгкой руки художников, которые где-то за рамкой картины выбирают три точки схода и делают, чтобы продолжения линий пересекались в этих трёх точках. Разумеется, компьютер никаких точек схода не расставляет — они получаются автоматически, если честно прокрутить 3D-расчёты.

3D использовалось в серии Final Fantasy эпохи PSX (VII—IX) для трехмерных моделей героев, монстров и NPC, а также фонов в боевых сценах; для всего остального использовались нарисованные в той же проекции статичные 2D-задники. Начиная с десятки, серия стала полностью трёхмерной и лишилась прибитой гвоздями камеры.

Сейчас, с засильем 3D, часто делают игры в перспективных проекциях, похожих на традиционные плоскую или изометрическую: WarCraft III, StarCraft II… Хотя часто это приводит к противной дилемме: либо нужно показывать левую и правую границу поля, либо смириться, что доступ к объектам у этой границы будет затруднён (StarCraft II: Wings of Liberty, миссия «В кромешной тьме»).

«Первая попавшаяся» трёхмерная игра (BioShock)


Двухточечная (2,5D)

Двухточечная перспектива

Если картинная плоскость вертикальна, любая вертикальная прямая останется вертикальной (остаются только две точки схода). Опыт художников показывает, что наш мозг успешно корректирует вертикальную перспективу, и здания и интерьеры, показанные в статике в трёхточечной проекции, смотрятся плохо. Поэтому на картинах делают только две точки схода, а вертикальные линии оставляют вертикальными. Фотографы, снимающие здания, корректируют перспективу фотошопом или шифт-объективом.

А чем она интересна для нас, геймеров? А тем, что в годы с 1992 по 1996 она процветала в 3D-играх. Wolfenstein 3D, Doom, Duke Nukem 3D и многие другие трёхмерные игры того времени использовали двухточечную проекцию и рисовали стены по столбцам, а полы — по строкам.

Основная статья: Псевдотрёхмерность


Одноточечная

Atic Atac — здание в одноточечной проекции (для экономии памяти изрядно «поломанной»), а персонажи внезапно с видом сбоку.

Последняя разновидность перспективной проекции — когда картинной плоскости параллельны аж два ребра (то есть, одна грань). Раз две точки схода удалены в бесконечность, остаётся только одна — в направлении взгляда (обычно, но не обязательно, в центре картины).

В 2D-играх одноточечной перспективой делают только внутренности зданий. Персонажей и объекты обычно рисуют в проекции «три четверти» или боковой — даже если взгляд сверху вниз. Естественно, перспектива пригодна в основном для поэкранного фона; чтобы на прокручивающемся фоне артефакты не были заметны, художнику нужно хорошее чувство перспективы.

Современные ремейки классических игр (Prince of Persia Classic, Duck Tales Remastered) переводят в 3D с одноточечной проекцией.

Ещё примеры.

  • Prince of Persia 2: The Shadow and the Flame выполнена в традиционной диметрии с плоскими спрайтами, но одна из сцен на движке — «Avenge us! Avenge us!» — в одноточечной перспективе.
  • Another World в отдельных экранах использует одноточечную перспективу.
  • Существуют и псевдотрёхмерные игры с одноточечной проекцией, наиболее известные из них Grand Theft Auto 1 и 2.

Ещё раз.

Проекция Для художника Для компьютера Жанры
Трёхточечная Три точки схода Настоящее 3D Все
Двухточечная Две точки схода Картинная плоскость параллельна одной из осей 3D-шутеры 90-х
Одноточечная Одна точка схода Картинная плоскость параллельна двум осям Поэкранные аркады 80-х
Современные платформеры


Ломаная перспектива

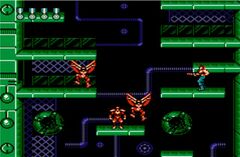
Ломаная проекция в Super Contra. Стены — попытались сделать какую-то перспективу, края платформ — «три четверти», узор на платформе — диметрия.

В ломаной проекции вообще нет проецирующих прямых: одни объекты проецируются так, другие этак. Это неплохо разнообразит 2D-игру, однако требует от художника опыта: нужно чувствовать перспективу и понимать габариты экрана, знать, что игрок увидит часто, что — редко, а что — вообще не увидит.

Причин «поломать» проекцию много.

  • Художественные причины:
    • Чтобы сгладить искажения проекции. Шар в любой косой проекции будет эллипсом — так, понятное дело, нельзя, мячик должен быть круглым. Atic Atac (см. выше) явно «снят широкоугольным объективом», и по краям «кадра» искажения будут слишком велики. Потому картины переданы в другой проекции.
    • Чтобы передать смену проекции при прокрутке уровня.
    • Для небольших предметов, которые невозможно нарисовать в такой проекции. Правда, если у машины широкая палитра, можно попробовать передать проекцию удачным тонированием.
    • И просто «желание левой задней пятки художника» aka «художественная выразительность».
  • Технические причины:

Обратная перспектива, распространённая в средневековой иллюстрации и иконописи, тоже ломаная. Изредка её используют и в играх — для построек намного больших, чем экран. В жизни подобие обратной перспективы встречается, если какой-нибудь объект находится в сантиметрах от носа — между глаз.

Параллаксная (многослойная) прокрутка

Кто не играл в «Аладдина» на «сеге»? Обратите внимание на барханы и облака на заднем плане — это один слой, но с фирменной «полосатой» прокруткой

Параллакс — это видимое смещение объектов друг относительно друга, когда смещается зритель. Самый впечатляющий параллакс будет, если посмотреть из окна автобуса или поезда. Следующий наш метод моделирует это явление.

Устроена параллаксная прокрутка несложно, этот метод освоили ещё мультипликаторы. Берём несколько слоёв (все, кроме нижнего — с прозрачными «дырками») и перемещаем их с разной скоростью, получается неплохая иллюзия перспективы. Сами же слои редко делают перспективными — обычно в какой-нибудь из параллельных проекций.

Super Nintendo (он же SNES) позволял до четырёх слоёв, Sega Megadrive (она же Sega Genesis) — всего два, но могла независимо прокручивать полосы фона[6]. На ПК многослойная прокрутка возможна, начиная с 386-х машин[7]. Из JavaME-телефонов (во времена их максимального распространения, середина 2000-х) многослойную прокрутку поддерживали только самые шустрые[8].

В квестах фирмы Daedalic Entertainment (The Whispered World, Deponia) таких слоёв может быть более десятка. Правда, это уже 2000-е годы…

В 3D параллакс получается автоматически. Однако, чтобы не рисовать много далёких объектов, используют так называемый скайбокс — большой задник, малоподвижный по сравнению со всеми остальными игровыми объектами. Старые FPS наподобие Doom заливали экран особой текстурой, когда движок попадал на «небесные» стены. В современных играх скайбокс — очень отдалённый, но существующий в геометрии уровней задник.

Нелинейные искажения

Двухмерные игры искажают крайне редко, в основном как спецэффект. В трёхмерных же…

  • Искажения под простенькую оптику шлемов виртуальной реальности (Oculus Rift и подобные).
  • Искажения под искривлённые мониторы.
  • Имитация плохой оптики (множество оптических приборов Myst, шлем Большого Папочки в BioShock).

С развитием шейдеров стали делать локальные искажения, связанные с преломлением в воде или перегретом воздухе — но это уже не проекция.

Трактат о неквадратном пикселе

Выше много раз говорилось: пиксель неквадратный, должно быть вытянуто (или, наоборот, приплюснуто) по вертикали. А почему оно так? Вкратце: ориентация на телевизор и ориентация на текст.

Давайте посмотрим несколько распространённых на то время машин (пропорция =1 — квадратный пиксель, >1 — стоячий пиксель, <1 — лежачий).[9]

Машина/видеорежим Назначение Вывод на ТВ Разрешение Пропорция
ZX Spectrum Бытовой компьютер PAL 256×192 1
BBC Micro режим 1 Бытовой/учебный комп. PAL 320×256 0,94
BBC Micro режим 0 PAL 640×256 1,88
IBM CGA/VGA Деловой компьютер NTSC (CGA) 320×200 1,2
IBM EGA Нет 640×350 1,37
IBM VGA (16 цветов) Нет 640×480 1
IBM CGA (текстовый) NTSC 640×200 2,4
IBM VGA (текстовый) Нет 720×400 1,35
Apple Macintosh Издательский компьютер Нет 512×342 1
Amiga (LowRes) Бытовой компьютер PAL[10] 320×256 0,94
Amiga (HiRes) PAL[10] 640×256 1,88
Nintendo NES/Dendy Игровая приставка NTSC[11] 256×240 0,8
Sega Genesis/Megadrive Игровая приставка NTSC[11] 320×224 1
Nintendo SNES Игровая приставка NTSC[11] 256×224 0,8

В PAL- и SÉCAM-машинах около 256 строк, в NTSC- — начиная с 200: одна строка пикселей — это две строки телевизионной развёртки. Горизонтальное же разрешение — столько, сколько вытягивает техника, обычно поменьше, потому и лежачий пиксель. Sega с квадратным пикселем выглядит «монстром» на фоне других машин. К тому же у телевизора развёртка чересстрочная и пиксельное тонирование будет адски полыхать — поэтому в полное телевизионное разрешение вышли уже тогда, когда truecolor-режимы сделали эти «изыски» ненужными (PlayStation, 1995).

Компьютерам приходится работать с текстом, поэтому горизонтальное разрешение важнее вертикального — а значит, стоячий пиксель. Правда, мониторы могут свободно перестраивать развёртку и потому не привязаны к 200 (или 256) строкам. В крупных шрифтах (например, в шрифтах для текстовых режимов в 8px шириной) вертикальные штрихи делали двухпиксельными.

А что же Macintosh, явно выбивающийся из нашей таблицы? Кинескоп у него обычный, 4:3. Но он намеренно не использовал полную площадь трубки, чтобы пиксель был в точности квадратный, а плотность была 72 пикселя на дюйм — для удобства настольного издательства. Впоследствии привязка к 72 ppi[12] сильно ударила по Apple (в Windows, например, принято 96 ppi, но не столь жёстко[13]) — но это уже середина 1990-х.[14].

Техническое отступление. Развёртка — это процесс управления электронным лучом приёмной телевизионной трубки (кинескопа). Луч строка за строкой проходит по всему экрану, строя изображение. Развёртка бывает построчной, или прогрессивной (каждый кадр развёртываются все строки одна за другой), и чересстрочной (первый полукадр развёртываются строки 1, 3, 5, 7 и т. д., второй полукадр — 2, 4, 6, 8…).

Примечания

  1. ↑ Если быть точным, cos α, который даже для 30° будет 0,86. Малая грань уже 0,5 — а большая всё ещё 0,86!
  2. ↑ = arctg[ 0,5·320·3 / (200·4) ]. Коэффициенты 3 и 4 — из соотношения сторон экрана 4:3.
  3. ↑ Кто чертил: ось X, которая во фронтальной проекции горизонтальная, в ортогональной наклонена на 7°.
  4. ↑ Конечно, имеются в виду приставки и компьютеры тех времён (начало 90-х). 640×480 VGA, 800×600 SVGA и всё, что появилось позднее — это белые и пушистые квадратные пиксели.
  5. ↑ Анимация, когда персонаж состоит из плоских сочленённых деталей, как картонная кукла. Детали могут быть нежёсткими и деформироваться (как в портретах Dust: An Elysian Tail).
  6. ↑ По поводу того, чем приставки отличаются от ПК: статья, перевод
  7. ↑ Скроллинг был и на «двойках» (Golden Axe), но делался он хитрым перепрограммированием VGA по рецептам небезызвестного Майкла Абраша и не позволял «дыр». Другими словами, однослойный. А на полную перерисовку экрана 286-м не хватало пропускной способности шины.
  8. ↑ То же самое: особым образом забуферизировав фон, можно наладить очень быструю прокрутку, даже на Samsung C100 дававшую ≈8 fps — но без дыр.
  9. ↑ Методика подсчёта: 0,75·ширина/высота. Для всех японских NTSC-приставок берётся высота 240 (приставкам нужно изображение без рамки, а полный NTSC-растр составляет 483 строки). Об Apple см. в тексте.
  10. ↑ 10,0 10,1 В NTSC-версиях «Амиги» разрешение ниже.
  11. ↑ 11,0 11,1 11,2 Впоследствии появились и PAL-версии с меньшими вылетами изображения (телевизионный термин, часть телесигнала, скрытая за пределами экрана).
  12. ↑ Pixels per inch, пикселей на дюйм.
  13. ↑ Хотя программирование под большие PPI — такой ещё ад, не зря в Windows 7 придумали виртуализацию PPI (программа должна сказать: «Я поддерживаю высокую плотность пикселей», иначе Windows её отрендерит на стандартной и растянет). Но хотя бы разработчики крупного ПО этот ад знают и проходят.
  14. ↑ Ководство, § 70. Разрешение экранов. И немного о происхождении 72 точек на дюйм.
[изменить]
Видеоигры
ЖанрыЗелёным выделены те, для которых есть отдельные шаблоны Ролевая компьютерная игра (С сражениями/Immersive sim • Dungeon Crawl • С сражениями холодным оружием • С японской спецификой • Многопользовательская • Privateer • Roguelike • Roguelite • Souls-like • Тактическая) • Survival Horror • 4X-стратегии • Абстрактная игра • Варгейм • Визуальные романы • Головоломки (Puzzle-platformer • головоломка от первого лица) • Инженерный конструктор (Cosmoteer) • Интерактивные мультфильмы • Интерактивные фильмы • Казуальные игры (Игровой автомат • Мобильный гейминг • Runner game • Tower Defence • Zuma и Luxor) • Квесты (Я ищу) • «Королевская битва» • Платформеры (Puzzle-platformer • метроидвания) • Пошаговые стратегии (Герои не меча и не магии) • Симуляторы (Экономические) • Shoot'em up (Шутеры (От первого лица • Про войну) • Стелс-экшен • Стратегии в реальном времени (MOBA • стратегия непрямого контроля • Тактика в реальном времени • экономическая стратегия) • Beat 'em up (Файтинги) • Экшн-триллеры • Idle game • Мешанина жанров • Инди-игры • Прочее (Covetous • osu!)
Геймплейные архетипыВсе видеоигры — это 8-битки • Геймплей от X-COM • Есть геймплей — сюжет не нужен vs Есть сюжет — геймплей не нужен • Лутоцентричная игра • Песочница • Суповой набор от Bioware
АмплуаБезликий протагонист (бесплотный генерал) • Безымянный герой • Бесполезный советчик • Боевой наркоман • Бывшие нейтралы • Виртуальная пассия (гей-вариант) • Герой в радужных доспехах • Гумба • Девушка-геймер • Единственный человек в цеху • Закадровый штурман • Какой ещё боевой путь? • Манчкин/Пауэрплеер • Металлический слизень • Не героические тактические роли (Лицехват • Моб-вредитель • Моб-грабитель) • Никакой не приключенец • Скальный наездник (Рыба-кусака) • Неигровая злодейская фракция • Союзники не к месту • Странствующий герой • Суперстража • Торговец не к месту • Уникальный головорез • Ходячий IDDQD • Этот гадкий hitscan-пулемётчик
Тактические ролиБуквальный джаггернаут • Выходила на берег Катюша • Гарпунщик • Джаггернаут • Крепкий середнячок • Реактивный громила • Стеклянная пушка • Супер-юнит • Танк (автономный • консервная банка • мамонт-танк • недотанк) • Хлипкий маг • Хрупкий шустрик
БоссыВынесено в отдельный шаблон Пока в процессе перепиливания.
ПерсонажиGuest character • NPC (NPC не воруют • NPC не трусят!) • Автоматическая турель • Несколько игровых персонажей • Поиграй пока вот этим (Игра за злодея • Игра за негуманоида • Игровой антропоцентризм) • Редактор внешности персонажа
Уровни/архитектураАвтоскроллинг-троллинг • Бесхозный станковый пулемёт • Благосклонная архитектура • Взрывающиеся бочки • Внутри меньше, чем снаружи • Волшебная лесопилка • Вышки в Open-world • Дай покататься! • Данж (гайгэксианское подземелье • желудочно-кишечный тракт • лабиринт • нубская пещера • освещённые подземелья • Очевидно зловещий последний данж • уровень-утроба) • Злонамеренная архитектура • Карманный Сусанин • Карта локаций/Сеть телепортов • Корзина для мусора • Край уровня • Ключи и двери (взаимозаменяемые ключи из антивещества) • Летать через кольца • Лоскутная география • Лунный уровень • Невидимая стена vs Ложная стена • Нубская песочница • Новый старый уровень • Обвалившийся мост • Паркур • Плоская архитектура • Подводный уровень • Предупредительная архитектура • Прыжковая головоломка • Прыжок веры • Рушится царство кощеево • Секретка (секрет святого Рандомия) • Скелет в шкафу • Склад • Смертельная яма • Стражник сторожит стену • Совсем не уникальная задача • Сюжетный гранатомёт • Терминаторизатор • Точка невозврата • Туториал • Уровень-качалка • Уровень-передышка • Штаб-квартира игрока • Этот гадкий уровень/Эта гадкая карта
ГрафикаHUD • Motion capture • Анимация простоя • Блики объектива • Брюки без границ • Вид (Вид от сапога • От первого лица/призрак от первого лица • От третьего лица) • Видеовставка • Всегда чистый • Двурукий спрайт • Дистанционный туман • Зловещая долина • Испаряющиеся трупы • Графон как в Крузисе vs Графон не нужен • Круг позора • Модели освещения • Мониторный угол зрения • Не хватает черт лица • Перескиновка • Получен предмет! • Проекции графики • Псевдотрёхмерность • Смена палитры • Спецдефекты • Стили графики • Тайлсет • Фальшивый камуфляж • Цел-шейдинг • Юниты не в масштабе • Экран загрузки
ФизикаАвтопилот • Адамантовый блок • Бежать по диагонали • Бесконечный боезапас • Взрывающийся вертолёт • Время не в масштабе • Воздух — это земля • Гравитационная пушка • Граната поражает вблизи • Гранату бросить нелегко • Двойной прыжок • Добежать до пулемётчика за ход • Забыли про гравитацию • Капюшон мгновенного облысения • Лезть через забор без рук • Небьющиеся лампочки • Неизменяемый ландшафт • Неприступный заборчик • Один хитбар на всё • Плавать в доспехе • Плавать в лаве • Подпрыгнув, присесть • Пуленепробиваемый картон • Ракета летит медленно • Распрыжка • Рокет-джамп • Рэгдолл • Снайперский пистолет • Стрельба из гранатомёта в комнате • Танк имеет много хитов • Физическая головоломка • Хлипкий всадник • Хитбокс
ИИАвтобой • Автодогон • Автоприцел • Идиотская дипломатия • ИИ ненавидит игрока • ИИ этим не пользуется • Искусственный идиот (Обезьяна с гранатой • Топографический кретинизм у ИИ) vs Искусственный гений • Лобовая атака • Полуслепые стражники • Универсальный скупщик • Читерский ИИ (Всевидящий ИИ) • Эскорт-миссия
Сетевая и онлайнDeathmatch • Free to Pay/Free to Play • Full Invasion • PvE • PvP • Армия Избранных • Баг (багоюзерство) • Бот • Вредительство vs. Антивредительская фича • Ганк • Донат • Захват флага • Игра на победу • Каждому игроку по Леголасу! • Кемпер • Киберспорт • Классификация MMO-игроков по Бартлу • Контра • Кооперативная игра • Нуб • Победа на старте • Сессионка • Твинк • Фраг • Читерство • Чиз
ДвижкиBuild • idtech (Doom • Wolfenstein 3D) • LithTech • NetImmerse • RPG Maker • Source • Unreal
КритикаAngry Video Game Nerd • Игрожур
←Навигация • Понятия видеоигр
Источник — http://posmotreli.su/index.php?title=Проекции_графики&oldid=1660